3.3. Discrimination

ROC Curve (Receiver Operating Characteristic Curve)

A Receiver Operating Characteristic curve, often referred to as the ROC curve, is a graphical plot that illustrates the diagnostic ability of a binary classifier system as its discrimination threshold is varied. The ROC curve is created by plotting the True Positive Rate (TPR) against the False Positive Rate (FPR) at various threshold settings.

import numpy as np
import pandas as pd

np.random.seed(0)

import xgboost as xgb
from matplotlib import pyplot as plt
from sklearn.datasets import make_classification
from sklearn.metrics import confusion_matrix, roc_auc_score, roc_curve
from sklearn.model_selection import train_test_split

%matplotlib inline

%config InlineBackend.figure_format = 'retina'

# Generate a synthetic dataset

X, y = make_classification(
    n_samples=50000,
    n_features=15,
    weights=[0.90, 0.10],
    n_classes=2,
    n_informative=5,
    random_state=42,
)

X, y = pd.DataFrame(X), pd.DataFrame(y)

X.columns = [f"feature_{i+1}" for i in range(len(X.columns))]

ix_train, ix_test = train_test_split(X.index, stratify=y, random_state=62)

# Create an XGBoost model with random forests
model_gbdt = xgb.XGBClassifier(
    booster="gbtree",
    max_depth=3,
    subsample=0.5,
    colsample_bynode=0.2,
    eval_metric=["logloss", "auc"],
    early_stopping_rounds=10,
)

evalset = [(X.loc[ix_train], y.loc[ix_train]), (X.loc[ix_test], y.loc[ix_test])]

# Fit the model to the generated dataset
model_gbdt.fit(X.loc[ix_train], y.loc[ix_train], eval_set=evalset)

[0]	validation_0-logloss:0.31868	validation_0-auc:0.74799	validation_1-logloss:0.32003	validation_1-auc:0.73429
[1]	validation_0-logloss:0.31147	validation_0-auc:0.77143	validation_1-logloss:0.31330	validation_1-auc:0.75790
[2]	validation_0-logloss:0.29090	validation_0-auc:0.80875	validation_1-logloss:0.29277	validation_1-auc:0.79646
[3]	validation_0-logloss:0.25391	validation_0-auc:0.87448	validation_1-logloss:0.25929	validation_1-auc:0.85711
[4]	validation_0-logloss:0.23867	validation_0-auc:0.87743	validation_1-logloss:0.24538	validation_1-auc:0.86018
[5]	validation_0-logloss:0.23249	validation_0-auc:0.87962	validation_1-logloss:0.23899	validation_1-auc:0.86309
[6]	validation_0-logloss:0.22075	validation_0-auc:0.88028	validation_1-logloss:0.22876	validation_1-auc:0.86379
[7]	validation_0-logloss:0.20951	validation_0-auc:0.88844	validation_1-logloss:0.21681	validation_1-auc:0.87391
[8]	validation_0-logloss:0.20340	validation_0-auc:0.89566	validation_1-logloss:0.21060	validation_1-auc:0.88160
[9]	validation_0-logloss:0.19451	validation_0-auc:0.90646	validation_1-logloss:0.20321	validation_1-auc:0.89147
[10]	validation_0-logloss:0.18822	validation_0-auc:0.90784	validation_1-logloss:0.19768	validation_1-auc:0.89276
[11]	validation_0-logloss:0.18632	validation_0-auc:0.90870	validation_1-logloss:0.19591	validation_1-auc:0.89392
[12]	validation_0-logloss:0.18271	validation_0-auc:0.91054	validation_1-logloss:0.19230	validation_1-auc:0.89655
[13]	validation_0-logloss:0.17151	validation_0-auc:0.91748	validation_1-logloss:0.18161	validation_1-auc:0.90503
[14]	validation_0-logloss:0.16778	validation_0-auc:0.92028	validation_1-logloss:0.17812	validation_1-auc:0.90811
[15]	validation_0-logloss:0.16652	validation_0-auc:0.92346	validation_1-logloss:0.17703	validation_1-auc:0.91141
[16]	validation_0-logloss:0.16468	validation_0-auc:0.92403	validation_1-logloss:0.17518	validation_1-auc:0.91224
[17]	validation_0-logloss:0.16159	validation_0-auc:0.92810	validation_1-logloss:0.17206	validation_1-auc:0.91620
[18]	validation_0-logloss:0.15828	validation_0-auc:0.93233	validation_1-logloss:0.16814	validation_1-auc:0.92143
[19]	validation_0-logloss:0.15637	validation_0-auc:0.93266	validation_1-logloss:0.16663	validation_1-auc:0.92141
[20]	validation_0-logloss:0.15157	validation_0-auc:0.93809	validation_1-logloss:0.16189	validation_1-auc:0.92716
[21]	validation_0-logloss:0.15019	validation_0-auc:0.94001	validation_1-logloss:0.16036	validation_1-auc:0.92986
[22]	validation_0-logloss:0.14763	validation_0-auc:0.94201	validation_1-logloss:0.15787	validation_1-auc:0.93161
[23]	validation_0-logloss:0.14683	validation_0-auc:0.94312	validation_1-logloss:0.15725	validation_1-auc:0.93254
[24]	validation_0-logloss:0.14649	validation_0-auc:0.94300	validation_1-logloss:0.15711	validation_1-auc:0.93215
[25]	validation_0-logloss:0.14497	validation_0-auc:0.94405	validation_1-logloss:0.15576	validation_1-auc:0.93276
[26]	validation_0-logloss:0.14438	validation_0-auc:0.94412	validation_1-logloss:0.15540	validation_1-auc:0.93225
[27]	validation_0-logloss:0.14372	validation_0-auc:0.94514	validation_1-logloss:0.15473	validation_1-auc:0.93327
[28]	validation_0-logloss:0.14293	validation_0-auc:0.94524	validation_1-logloss:0.15389	validation_1-auc:0.93358
[29]	validation_0-logloss:0.14181	validation_0-auc:0.94640	validation_1-logloss:0.15264	validation_1-auc:0.93522
[30]	validation_0-logloss:0.14124	validation_0-auc:0.94732	validation_1-logloss:0.15194	validation_1-auc:0.93615
[31]	validation_0-logloss:0.14067	validation_0-auc:0.94754	validation_1-logloss:0.15164	validation_1-auc:0.93659
[32]	validation_0-logloss:0.13768	validation_0-auc:0.94923	validation_1-logloss:0.14873	validation_1-auc:0.93882
[33]	validation_0-logloss:0.13700	validation_0-auc:0.94980	validation_1-logloss:0.14807	validation_1-auc:0.93935
[34]	validation_0-logloss:0.13583	validation_0-auc:0.95112	validation_1-logloss:0.14707	validation_1-auc:0.94033
[35]	validation_0-logloss:0.13547	validation_0-auc:0.95109	validation_1-logloss:0.14677	validation_1-auc:0.94021
[36]	validation_0-logloss:0.13478	validation_0-auc:0.95185	validation_1-logloss:0.14616	validation_1-auc:0.94084
[37]	validation_0-logloss:0.13438	validation_0-auc:0.95207	validation_1-logloss:0.14566	validation_1-auc:0.94175
[38]	validation_0-logloss:0.13321	validation_0-auc:0.95237	validation_1-logloss:0.14457	validation_1-auc:0.94193
[39]	validation_0-logloss:0.13247	validation_0-auc:0.95248	validation_1-logloss:0.14407	validation_1-auc:0.94214
[40]	validation_0-logloss:0.13169	validation_0-auc:0.95313	validation_1-logloss:0.14343	validation_1-auc:0.94244
[41]	validation_0-logloss:0.13139	validation_0-auc:0.95371	validation_1-logloss:0.14339	validation_1-auc:0.94261
[42]	validation_0-logloss:0.13113	validation_0-auc:0.95391	validation_1-logloss:0.14316	validation_1-auc:0.94302
[43]	validation_0-logloss:0.12623	validation_0-auc:0.95643	validation_1-logloss:0.13890	validation_1-auc:0.94591
[44]	validation_0-logloss:0.12470	validation_0-auc:0.95712	validation_1-logloss:0.13783	validation_1-auc:0.94638
[45]	validation_0-logloss:0.12441	validation_0-auc:0.95745	validation_1-logloss:0.13771	validation_1-auc:0.94619
[46]	validation_0-logloss:0.12365	validation_0-auc:0.95841	validation_1-logloss:0.13739	validation_1-auc:0.94652
[47]	validation_0-logloss:0.12301	validation_0-auc:0.95895	validation_1-logloss:0.13697	validation_1-auc:0.94669
[48]	validation_0-logloss:0.12173	validation_0-auc:0.95932	validation_1-logloss:0.13588	validation_1-auc:0.94721
[49]	validation_0-logloss:0.12075	validation_0-auc:0.96029	validation_1-logloss:0.13494	validation_1-auc:0.94837
[50]	validation_0-logloss:0.11699	validation_0-auc:0.96234	validation_1-logloss:0.13082	validation_1-auc:0.95033
[51]	validation_0-logloss:0.11694	validation_0-auc:0.96240	validation_1-logloss:0.13076	validation_1-auc:0.95039
[52]	validation_0-logloss:0.11667	validation_0-auc:0.96245	validation_1-logloss:0.13069	validation_1-auc:0.95027
[53]	validation_0-logloss:0.11653	validation_0-auc:0.96258	validation_1-logloss:0.13071	validation_1-auc:0.95027
[54]	validation_0-logloss:0.11280	validation_0-auc:0.96470	validation_1-logloss:0.12685	validation_1-auc:0.95280
[55]	validation_0-logloss:0.11265	validation_0-auc:0.96468	validation_1-logloss:0.12677	validation_1-auc:0.95273
[56]	validation_0-logloss:0.11249	validation_0-auc:0.96485	validation_1-logloss:0.12675	validation_1-auc:0.95263
[57]	validation_0-logloss:0.11175	validation_0-auc:0.96511	validation_1-logloss:0.12645	validation_1-auc:0.95280
[58]	validation_0-logloss:0.11159	validation_0-auc:0.96528	validation_1-logloss:0.12644	validation_1-auc:0.95299
[59]	validation_0-logloss:0.11053	validation_0-auc:0.96588	validation_1-logloss:0.12551	validation_1-auc:0.95360
[60]	validation_0-logloss:0.10953	validation_0-auc:0.96661	validation_1-logloss:0.12410	validation_1-auc:0.95492
[61]	validation_0-logloss:0.10929	validation_0-auc:0.96669	validation_1-logloss:0.12410	validation_1-auc:0.95474
[62]	validation_0-logloss:0.10884	validation_0-auc:0.96690	validation_1-logloss:0.12409	validation_1-auc:0.95455
[63]	validation_0-logloss:0.10867	validation_0-auc:0.96707	validation_1-logloss:0.12413	validation_1-auc:0.95441
[64]	validation_0-logloss:0.10714	validation_0-auc:0.96794	validation_1-logloss:0.12296	validation_1-auc:0.95527
[65]	validation_0-logloss:0.10681	validation_0-auc:0.96827	validation_1-logloss:0.12257	validation_1-auc:0.95569
[66]	validation_0-logloss:0.10661	validation_0-auc:0.96830	validation_1-logloss:0.12263	validation_1-auc:0.95542
[67]	validation_0-logloss:0.10646	validation_0-auc:0.96841	validation_1-logloss:0.12258	validation_1-auc:0.95531
[68]	validation_0-logloss:0.10634	validation_0-auc:0.96859	validation_1-logloss:0.12253	validation_1-auc:0.95553
[69]	validation_0-logloss:0.10608	validation_0-auc:0.96867	validation_1-logloss:0.12227	validation_1-auc:0.95580
[70]	validation_0-logloss:0.10598	validation_0-auc:0.96875	validation_1-logloss:0.12241	validation_1-auc:0.95576
[71]	validation_0-logloss:0.10579	validation_0-auc:0.96898	validation_1-logloss:0.12235	validation_1-auc:0.95585
[72]	validation_0-logloss:0.10435	validation_0-auc:0.96956	validation_1-logloss:0.12086	validation_1-auc:0.95663
[73]	validation_0-logloss:0.10293	validation_0-auc:0.97004	validation_1-logloss:0.11963	validation_1-auc:0.95723
[74]	validation_0-logloss:0.10276	validation_0-auc:0.97012	validation_1-logloss:0.11971	validation_1-auc:0.95694
[75]	validation_0-logloss:0.10200	validation_0-auc:0.97053	validation_1-logloss:0.11893	validation_1-auc:0.95774
[76]	validation_0-logloss:0.10171	validation_0-auc:0.97062	validation_1-logloss:0.11876	validation_1-auc:0.95785
[77]	validation_0-logloss:0.10109	validation_0-auc:0.97073	validation_1-logloss:0.11803	validation_1-auc:0.95804
[78]	validation_0-logloss:0.10071	validation_0-auc:0.97073	validation_1-logloss:0.11815	validation_1-auc:0.95768
[79]	validation_0-logloss:0.10010	validation_0-auc:0.97098	validation_1-logloss:0.11758	validation_1-auc:0.95783
[80]	validation_0-logloss:0.10006	validation_0-auc:0.97093	validation_1-logloss:0.11756	validation_1-auc:0.95783
[81]	validation_0-logloss:0.09989	validation_0-auc:0.97105	validation_1-logloss:0.11743	validation_1-auc:0.95805
[82]	validation_0-logloss:0.09962	validation_0-auc:0.97129	validation_1-logloss:0.11725	validation_1-auc:0.95794
[83]	validation_0-logloss:0.09947	validation_0-auc:0.97167	validation_1-logloss:0.11727	validation_1-auc:0.95787
[84]	validation_0-logloss:0.09941	validation_0-auc:0.97172	validation_1-logloss:0.11736	validation_1-auc:0.95782
[85]	validation_0-logloss:0.09928	validation_0-auc:0.97186	validation_1-logloss:0.11740	validation_1-auc:0.95779
[86]	validation_0-logloss:0.09903	validation_0-auc:0.97202	validation_1-logloss:0.11724	validation_1-auc:0.95777
[87]	validation_0-logloss:0.09891	validation_0-auc:0.97198	validation_1-logloss:0.11712	validation_1-auc:0.95784
[88]	validation_0-logloss:0.09873	validation_0-auc:0.97225	validation_1-logloss:0.11713	validation_1-auc:0.95791
[89]	validation_0-logloss:0.09859	validation_0-auc:0.97238	validation_1-logloss:0.11716	validation_1-auc:0.95788
[90]	validation_0-logloss:0.09845	validation_0-auc:0.97253	validation_1-logloss:0.11708	validation_1-auc:0.95773
[91]	validation_0-logloss:0.09806	validation_0-auc:0.97273	validation_1-logloss:0.11670	validation_1-auc:0.95793

XGBClassifier(base_score=None, booster='gbtree', callbacks=None,
              colsample_bylevel=None, colsample_bynode=0.2,
              colsample_bytree=None, device=None, early_stopping_rounds=10,
              enable_categorical=False, eval_metric=['logloss', 'auc'],
              feature_types=None, gamma=None, grow_policy=None,
              importance_type=None, interaction_constraints=None,
              learning_rate=None, max_bin=None, max_cat_threshold=None,
              max_cat_to_onehot=None, max_delta_step=None, max_depth=3,
              max_leaves=None, min_child_weight=None, missing=nan,
              monotone_constraints=None, multi_strategy=None, n_estimators=None,
              n_jobs=None, num_parallel_tree=None, random_state=None, ...)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

def get_roc_curve(y_test, y_proba, delta=0.1):
    """
    Return the True Positive Rates (TPRs), False Positive Rates (FPRs),
    and the threshold values, seperated by delta.
    """
    thresh = list(np.arange(0, 1, delta)) + [1]
    TPRs = []
    FPRs = []
    y_pred = np.empty(y_proba.shape)
    for th in thresh:
        y_pred[y_proba < th] = 0
        y_pred[y_proba >= th] = 1

        # confusion matrix
        (TN, FP), (FN, TP) = confusion_matrix(y_test, y_pred)
        TPR = TP / (TP + FN)  # sensitivity
        FPR = FP / (FP + TN)  # 1 - specificity
        TPRs.append(TPR)
        FPRs.append(FPR)
    return FPRs, TPRs, thresh

Here, delta is the difference between each of the thresholds at which ROC curve is calculated.

delta = 0.001
y_proba = model_gbdt.predict_proba(X.loc[ix_test])[:, 1]
FPRs, TPRs, _ = get_roc_curve(y.loc[ix_test], y_proba, delta)

fig, axs = plt.subplots(1, 2, figsize=(12, 6))

# First subplot (Left side)
ax = axs[0]

# Calculate ROC curve for your data
FPRs, TPRs, _ = roc_curve(y.loc[ix_test], y_proba)

# Plot the ROC curve on the first subplot
ax.plot(FPRs, TPRs, color="g", lw=2, label="ROC curve")
ax.plot([0, 1], [0, 1], color="navy", lw=2, linestyle="--", label="Random")
ax.set_xlim([-0.05, 1.0])
ax.set_ylim([0.0, 1.05])
ax.set_xlabel("False Positive Rate")
ax.set_ylabel("True Positive Rate")
ax.set_title(f"ROC curve (threshold delta = {delta})")
ax.legend(loc="lower right")

# Second subplot (Right side)
ax = axs[1]

# Calculate ROC curve for sklearn implementation
FPRs, TPRs, _ = roc_curve(y.loc[ix_test], y_proba)

# Plot the ROC curve on the second subplot
ax.plot(FPRs, TPRs, color="red", lw=2, label="ROC curve")
ax.plot([0, 1], [0, 1], color="navy", lw=2, linestyle="--", label="Random")
ax.set_xlim([-0.05, 1.0])
ax.set_ylim([0.0, 1.05])
ax.set_xlabel("False Positive Rate")
ax.set_ylabel("True Positive Rate")
ax.set_title("Scikit-learn's ROC curve")
ax.legend(loc="lower right")

# Display the subplots
plt.tight_layout()
plt.show()

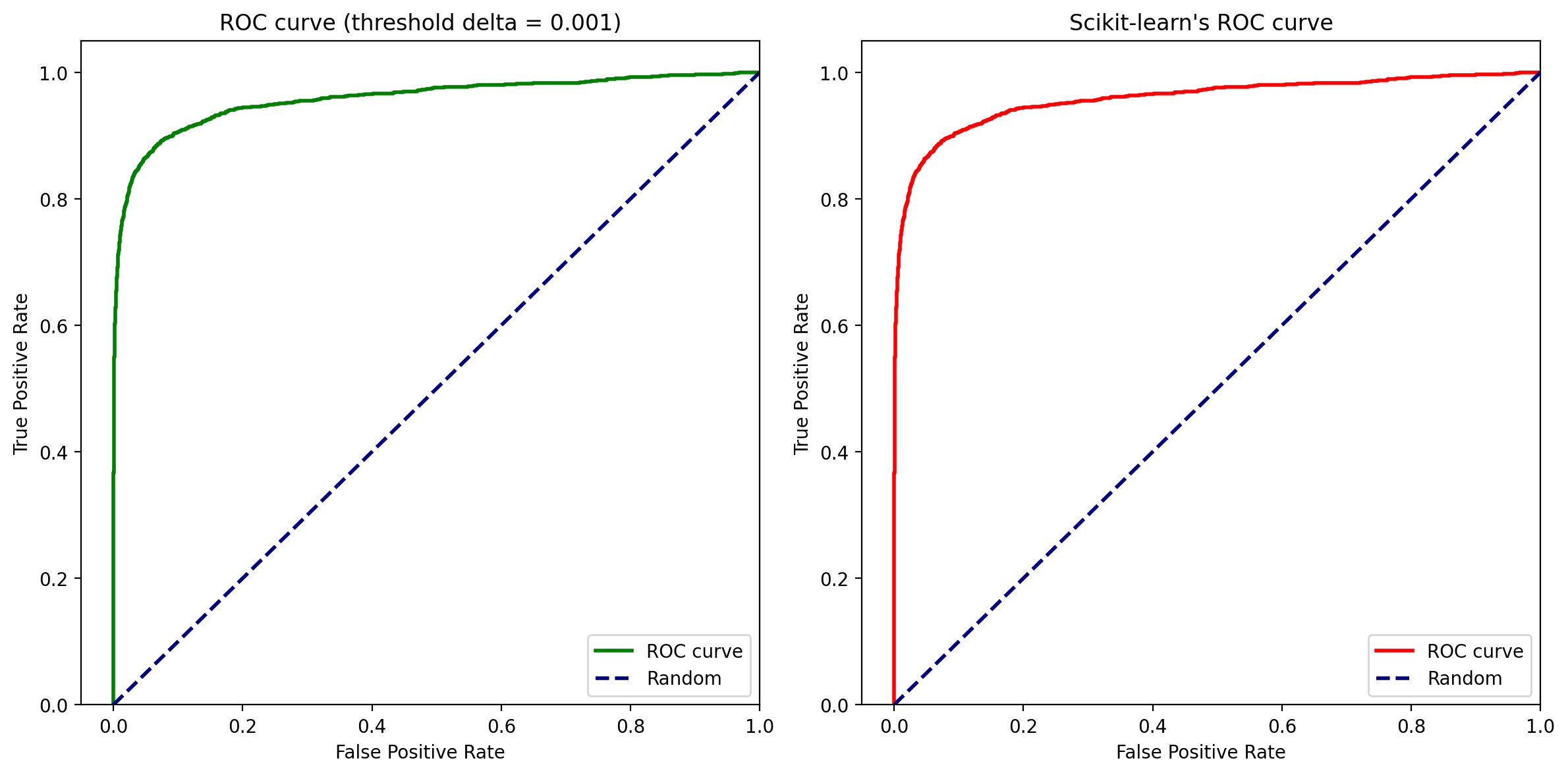
We can see that implementation of the ROC Curve is aligned with Scikit-Learn and gives consistent results.

Gini score

Now, that we know about ROC curve, AUC score and Gini score are straightforward to understand. AUC stands for Area under the Curve, which is nothing but the area under the ROC curve formed by the predictions. As we saw, a totally random prediction will have AUC score 0.5, while a perfect classifier will have AUC score of 1. The Gini score is a rescaled AUC score: Gini=AUC*2-1.

Lets check the AUC and Gini score of our model.

auc_score = roc_auc_score(y.loc[ix_test], y_proba)
print(f"AUC score: {auc_score: .4f}")
print(f"Gini score: {auc_score*2-1: .4f}")

AUC score:  0.9580
Gini score:  0.9161

Profit curve

Profit curve is an extension of ROC Curve analysis for cost-sensitive learning.

Prediction	Default +	Default -
Predicted Default +	{0} Correctly Predict Default	{-avg_profit} Falsely Predict Default
Predicted Default -	{-avg_loss} Falsely Predict Non-Default	{avg_profit} Correctly Predict Non-Default

# Define cost-benefit matrix based on observed losses and profits
# [tp, fp], [fn, tn]: [Loss incurred, Profit lost, Loss incurred, Profit made]
avg_profit, avg_loss = 1430, 1454
cost_benefit_matrix = np.array([[0, -avg_profit], [-avg_loss, avg_profit]])
print(cost_benefit_matrix)

[[    0 -1430]
 [-1454  1430]]

def standard_confusion_matrix(y_true, y_pred):
    """
    Reformat confusion matrix output from sklearn for plotting profit curve.
    """
    [[tn, fp], [fn, tp]] = confusion_matrix(y_true, y_pred)
    return np.array([[tp, fp], [fn, tn]])


def plot_profit_curve(
    cost_benefit_matrix, y_true: np.ndarray, y_proba: np.ndarray, **kwargs
):
    """
     Plot profit curve.

     Inputs:
     - model object
     - cost benefit matrix in the same format as the confusion matrix above
     - predicted probabilities
     - actual labels
    - additional kwargs for matplotlib
    """

    # Profit curve data
    profits = []  # one profit value for each T (threshold)
    thresholds = sorted(y_proba, reverse=True)

    # For each threshold, calculate profit - starting with largest threshold
    for T in thresholds:
        y_pred = (y_proba > T).astype(int)
        confusion_mat = standard_confusion_matrix(y_true, y_pred)
        # Calculate total profit for this threshold
        profit = sum(sum(confusion_mat * cost_benefit_matrix) / len(y_true))
        profits.append(profit)

    # Profit curve plot
    plt.plot(np.linspace(0, 1, len(y_true)), profits, **kwargs)

    return profits

plot_profit_curve_df = plot_profit_curve(
    cost_benefit_matrix,
    y.loc[ix_test],
    y_proba,
    color="fuchsia",
)

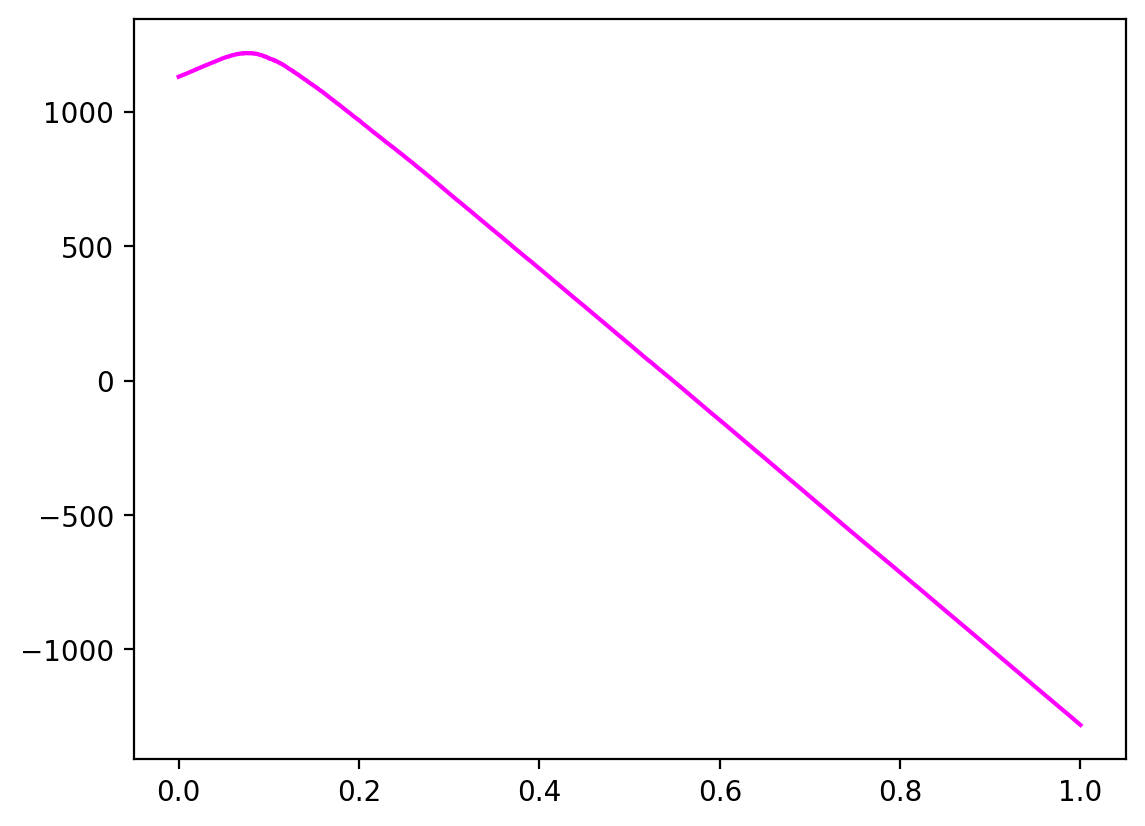
Somers' D score

Somers' D, often referred to as Somers' D statistic or Somers' Rank Correlation Coefficient, is a measure of the strength and direction of association between two ordinal variables. In case of binary classification, Somers'D and Gini score mean the same metric. For ordinal rankings, binning is recommended.

from scipy.stats import somersd
from sklearn.datasets import make_regression
from xgboost import XGBRFRegressor

# Create a synthetic regression dataset
X, y = make_regression(n_samples=10000, n_features=25, noise=100, random_state=0)

X, y = pd.DataFrame(X), pd.DataFrame(y)

X.columns = [f"feature_{i+1}" for i in range(len(X.columns))]

ix_train, ix_test = train_test_split(X.index, test_size=0.2, random_state=62)

xgb_rf = XGBRFRegressor(n_estimators=100, max_depth=10)
xgb_rf.fit(X.loc[ix_train], y.loc[ix_train])

XGBRFRegressor(base_score=None, booster=None, callbacks=None,
               colsample_bylevel=None, colsample_bytree=None, device=None,
               early_stopping_rounds=None, enable_categorical=False,
               eval_metric=None, feature_types=None, gamma=None,
               grow_policy=None, importance_type=None,
               interaction_constraints=None, max_bin=None,
               max_cat_threshold=None, max_cat_to_onehot=None,
               max_delta_step=None, max_depth=10, max_leaves=None,
               min_child_weight=None, missing=nan, monotone_constraints=None,
               multi_strategy=None, n_estimators=100, n_jobs=None,
               num_parallel_tree=None, objective='reg:squarederror',
               random_state=None, reg_alpha=None, ...)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

predictions = xgb_rf.predict(X.loc[ix_test])

# numpy cross-tab
contingency_table = np.histogram2d(
    y.loc[ix_test].values.flatten(), predictions.flatten(), bins=200
)[0]

res = somersd(contingency_table)
somers_d_score = res.statistic

print(f"gAUC score: {(somers_d_score + 1)/2:.2%}")
print(f"Somers' D score: {somers_d_score:.2%}")

gAUC score: 79.83%
Somers' D score: 59.66%

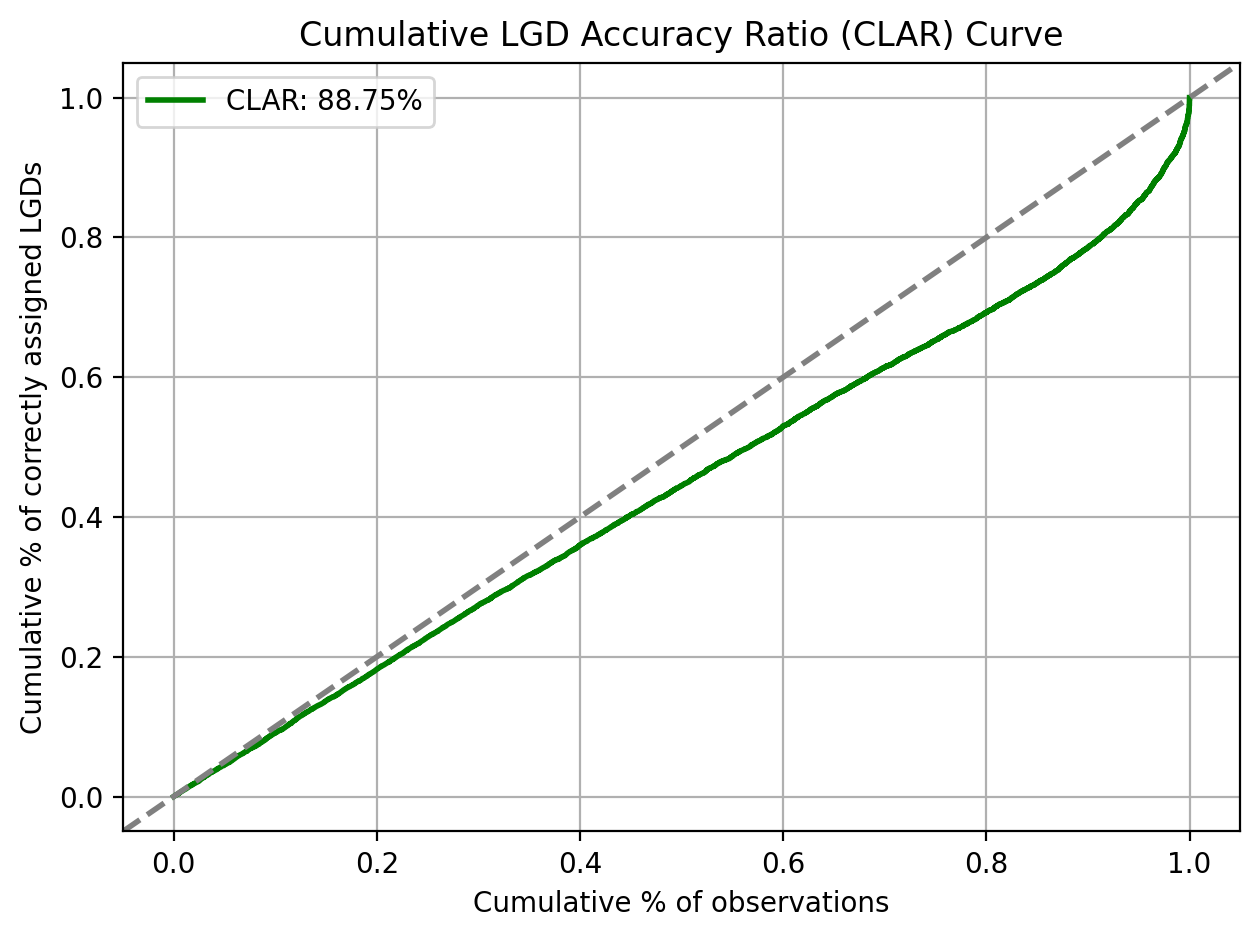
Cumulative LGD Accuracy Ratio (CLAR)

Adapted from VUROCS: Volume under the ROC Surface for Multi-Class ROC Analysis. For the purpose of discriminatory power assessment, the predicted and realised LGDs are usually mapped to a discretised LGD scale.

def clar(y: np.ndarray, X: np.ndarray) -> float:
    """Calculate Cumulative LGD Accuracy Ratio (CLAR).

    CLAR measures the ability of predicted LGD categories to discriminate
    realized LGD values according to Ozdemir and Miu 2009.

    Args:
        y (np.ndarray): Vector of realized LGD values
        X (np.ndarray): Vector of predicted LGD values

    Returns:
        CLAR value for the predicted and realized LGD categories (np.float)
        Share of observations as a numpy array (np.ndarray)
        Cumulative share of correctly assigned LGD values as a numpy array (np.ndarray)

    Raises:
        ValueError: If either 'X' or 'y' contains NA values
        ValueError: If 'X' and 'y' have different lengths

    References:
        Ozdemir, B., Miu, P., 2009. Basel II Implementation. A Guide to
        Developing and Validating a Compliant Internal Risk Rating System.
        McGraw-Hill, USA.
    """

    if any(pd.isna(X)) or any(pd.isna(y)):
        raise ValueError("Both 'X' and 'y' must not contain NA values")

    if len(X) != len(y):
        raise ValueError("Both 'X' and 'y' must be of the same length")

    nx = len(X)
    classes = sorted(list(set(X).union(set(y))), reverse=True)
    num = [sum(X == cls) for cls in classes]
    cnum = np.cumsum(num)
    index = np.argsort(X)[::-1]
    X = np.array(X)[index]
    y = np.array(y)[index]
    corr = np.zeros(len(classes))

    for i in range(len(classes) - 1):
        if cnum[i] > 0:
            corr[i] = np.sum(y[: cnum[i]] >= classes[i])

    corr /= nx
    corr[-1] = 1
    obs = cnum / nx

    res = obs[0] * corr[0] / 2
    for i in range(1, len(corr)):
        res += (corr[i] - corr[i - 1]) * (obs[i] - obs[i - 1]) / 2 + (
            obs[i] - obs[i - 1]
        ) * corr[i - 1]

    return res * 2, obs, corr

# generate a synthetic dataset
np.random.seed(0)

# Generate the first variable as random probabilities between 0 and 1
num_samples = 10000
lgd_observed = np.random.rand(num_samples)

# Create the second variable with a specified correlation to the first
correlation = 0.7  # correlation
lgd_predicted = correlation * lgd_observed + (1 - correlation) * np.random.rand(
    num_samples
)

# Ensure both variables are within the range [0, 1]
lgd_observed = np.clip(lgd_observed, 0, 1)
lgd_predicted = np.clip(lgd_predicted, 0, 1)

clar_score = clar(lgd_observed, lgd_predicted)[0]
print(f"CLAR: {clar_score:.4%}")

CLAR: 88.7468%

plt.figure()
plt.plot(
    clar(lgd_observed, lgd_predicted)[1],
    clar(lgd_observed, lgd_predicted)[2],
    color="g",
    linewidth=2,
    label=f"CLAR: {clar_score:.2%}",
)

# Add a horizontal line representing perfect discrimination
plt.axline((0, 0), slope=1, linestyle="--", linewidth=2, color="gray")

plt.xlabel("Cumulative % of observations")
plt.ylabel("Cumulative % of correctly assigned LGDs")
plt.title("Cumulative LGD Accuracy Ratio (CLAR) Curve")
plt.legend()

plt.grid(True)
plt.tight_layout()
plt.show()